研究例題

ここでは、実際に新しいことを発見するための例題を紹介します。例題は、私達のグループが行った研究を元にしています。

ここでの基本は、次の3つです。

1.適当な問題を見つける

2. それを解くのではなく、変形する　(問題が簡単な場合は解いてみる）

3. 変形した問題を調べる　(必要なら数学ソフトを使う。)

ここでは数学ソフトの活用については、省略しています。

次のような問題を考えます。

問題

箱の中に、１枚の赤と5枚の白のカードがあり、2人のプレイヤーが交互にカードを引き、どちらかのプレイヤーが赤のカードを引くと、そのプレイヤーが負け、そこでゲームが終わる。ただし、取り出したカードは箱に戻さない。

(元々は、ロシアンルーレットとして研究していました。)

問題の改変

与えられた問題を変えるために、問題の変えられる部分を赤色と青色にしました。

箱の中に、１枚の赤と5枚の白のカードがあり、2人のプレイヤーが交互にカードを引き、どちらかのプレイヤーが赤のカードを引くと、そのプレイヤーが負け、そこでゲームが終わる。ただし、取り出したカードは箱に戻さない。

赤の部分を変えると、数字の変更になります。

箱の中に、１枚の赤と5枚の白のカードがあり、2人のプレイヤーが交互にカードを引き、どちらかのプレイヤーが赤のカードを引くと、そのプレイヤーが負け、そこでゲームが終わる。

青の部分を変えると、ルール変更になります。

これまでに行った改変

これまで、私達の研究グループはこの問題の一部を変えることで、多くの研究成果を残してきました。

これまで行った問題の改変を、時代順に紹介します。これらは、結果的に数学の専門家の学会で通用するレベルまで達しました。

1992に当時の研究メンバーがここを変えてみました。

箱の中に、m枚の赤とn-m枚の白のカードがあり、2人のプレイヤーが交互にカードを引き、どちらかのプレイヤーが赤のカードを引くと、そのプレイヤーが負け、そこでゲームが終わる。

箱の中に、m枚の赤とn-m枚の白のカードがある場合に、先手のプレイヤーが負ける確率をf(n,m)として、

nとmを変化させて、以下のような三角形にしました。

これは、パスカルの三角形でnCmを並べるときと同じやり方です。

上のf(n,m)を全て計算すると次のようになります。

分数の分母と分子を比べてみると、それぞれがパスカルの三角形に似たものになっています。

例えば、青の三角形に入っている分数を見てください。

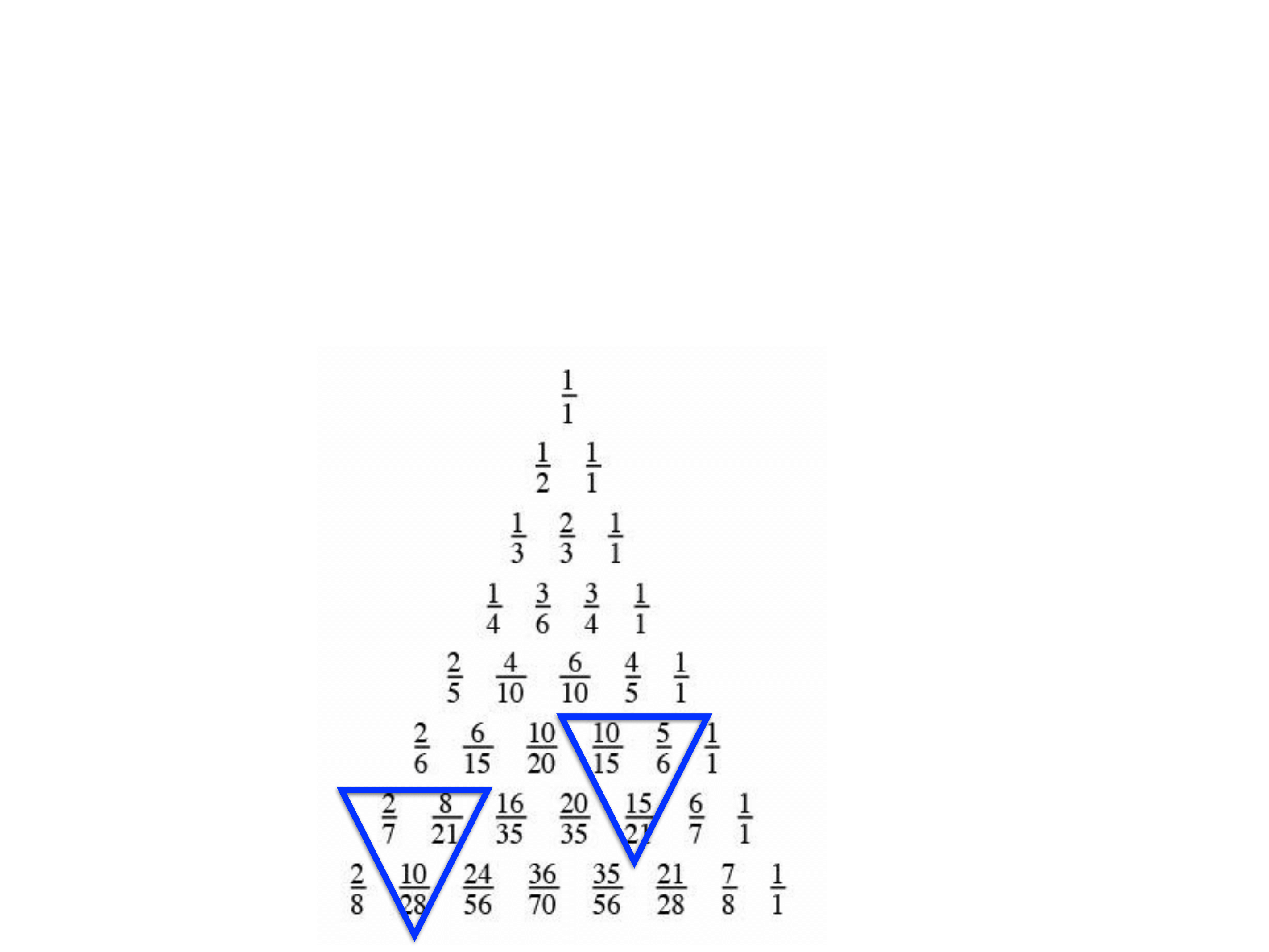
このパスカルの三角形に似た性質の証明はかなりシンプルです。

パスカルの三角形に似た分数というのが面白いと評価されて、雑誌「大阪数学教育雑誌」に掲載されました。

2007に当時の研究メンバーがプレイヤーの人数を2から自然数pに変えてみました。

↓

m枚の赤とn-m枚の白のカードがあり、プレイヤーがp人の場合を考えます。一番目のプレイヤーが負ける確率をf(p,n,m)として、

nとmを変化させて、以下のような三角形にしました。

f(p,n,m)をp=4として計算すると次のようになります。分数の分母と分子を比べるとそれぞれがパスカルの三角形に似たものになっています。

例えば、青の三角形に入っている分数を見てください。

pを一般の自然数にした場合、パスカルの三角形に似た性質の証明ができます。ここからさらに、。ここまでの研究が評価されて、イギリスの雑誌Mathematical Gazetteに掲載されました。

負ける条件の改変

もうこのくらいで、研究の限界かと思っていたのですが、まださらなる発展がありました。

変えられる部分はまだまだありました。

箱の中に、m枚の赤とn-m枚の白のカードがあり、2人のプレイヤーA,Bが交互にカードを引き、Aは赤のカードを1枚引くと負けるが、Bは赤のカードを２枚集めると負ける、そこでゲームが終わる。

2017に当時の研究メンバーが負ける条件をこのように変えてみました。

A,Bの負ける条件を変えているのがポイントです。

同じように１人目の人が負ける率を三角形状に書いてみると、面白いことが見つかりました。

それぞれがパスカルの三角形に似たものになっている場合と、そうでない場合があります。

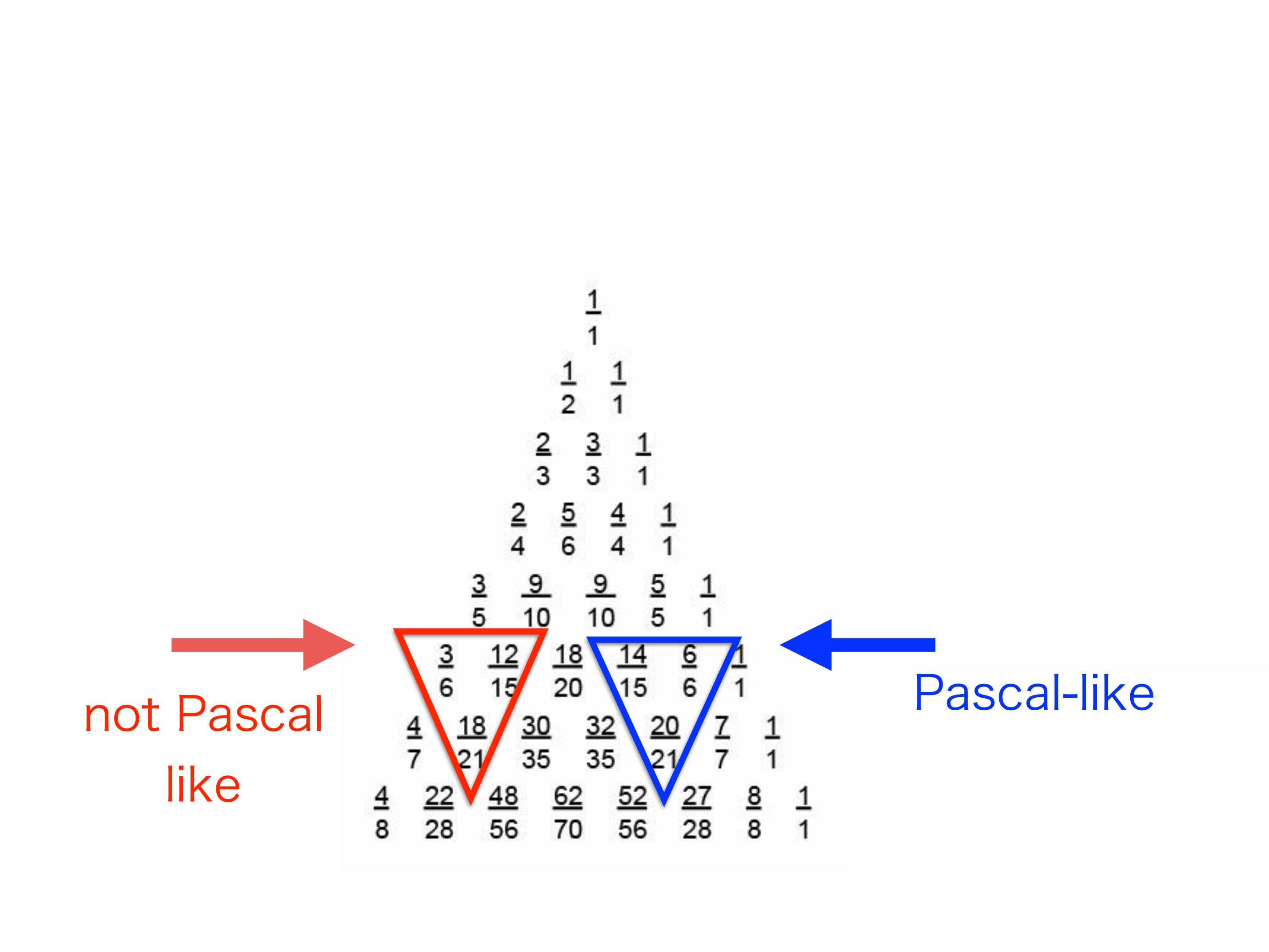
例えば、赤の三角形と青の三角形に入っている分数を見てください。

この分数の三角形の大部分で、パスカルの三角形的な法則が成立しますが、一定の周期で成立しない場所があります。

このことを証明して、数学系の国際学会

Japan Conference on Discrete and Computational Geometry, Graphs, and Games 2017に査読通過して発表しました。

順序の改変

問題文の中の変えられる部分はまだあるので、さらに変えてみると次のような問題ができました。

m枚の赤とn-m枚の白のカードがあり、2人のプレイヤーA,Bがカードを引き、どちらかのプレイヤーが赤のカードを引くと、そのプレイヤーが負け、そこでゲームが終わる。

2018年には、どのような順序で引くと

A,Bの負ける率が近くなるかを考えました。

プレイヤーAとBが、ABBABAAB, ...

という順でカードを引くと、二人の負け率が近くなり、カードの枚数を調整すると、全く等しくなることを発見しました。

このことを、Japan Conference on Discrete and Computational Geometry, Graphs, and Games 2018に査読通過して発表しました。

また、二人のプレイヤーAとBの負ける確率が同じになる場合を研究した結果、次のような新しい公式を発見しました。

この公式は既に学会誌に投稿しています。

ただし、+と−については次のように決めていきます。

(i)+, −, −, +
(ii)+,−,−,+,−,+,+,−

(iii)+,−,−,+,−,+,+,−,−,+,+,−,+,−,−,+

…

数学的解説

ここでは例題の中で扱った内容を数学的にもう少し詳しく扱います。

問題　　１枚の赤と5枚の白のカードがあり、2 人のプレイヤーA, Bが交互にカードを引き、どちらかのプレイヤーが赤のカードを引くと、そのプレイヤーが負け、そこでゲームが終わる。A,Bそれぞれが負ける確率を求めよ。

2人がそれそれ、A,B,A,B,A,Bという順で引きていくが、これを第1,2,3,4,5,6ラウンドと呼ぶ。第6ラウンドまでの勝負が決まることは明らか。

第1ラウンドでAが赤のカードを引いて負ける確率は である。第2ラウンドでBが負ける確率は、Aがまず第1ラウンドで白のカードを引き、それからBが赤のカードを引くのでとなる。

第3ラウンドでAが赤のカードを引いて負ける確率は、まずAが第1ラウンドで白のカードを引き、第2ラウンドでBが白のカードを引き、それからAが赤のカードを引くのでとなる。同じようにして第４ラウンドでBが負ける確率は、第5ラウンドでAが負ける確率は、第6ラウンドでBが負ける確率はとなる。

第3ラウンドでAが赤のカードを引いて負ける確率は、まずAが第1ラウンドで白のカードを引き、第2ラウンドでBが白のカードを引き、それからAが赤のカードを引くのでとなる。同じようにして第４ラウンドでBが負ける確率は、第5ラウンドでAが負ける確率は、第6ラウンドでBが負ける確率はとなる。

したがって、Aが負ける確率は、Bが負ける確率もとなる。

問題　　赤のカードがm枚と、白のカードがn-m枚あり、この中から2 人のプレイヤーA, Bが交互にカードを引き、どちらかのプレイヤーが赤のカードを引くと、そのプレイヤーが負け、そこでゲームが終わる。

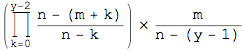この時、プレーはn-m+1ラウンドまで続く。第1ラウンドでAが負ける確率は, 第2ラウンドでBが負ける確率は, 第3ラウンドでAが負ける確率は,...,第yラウンドで勝負が決まる確率はとなる。

先手のAが負ける確率はで、Aがプレーするラウンド数は最大⌊⌋である。

補足　第yラウンドで勝負が決まる確率は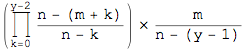となる。しかし、この計算は別のやり方がある。カードがn枚重ねられているとして、上から順番に引いているとする。ランダムに重ねる順番を決めると考える。

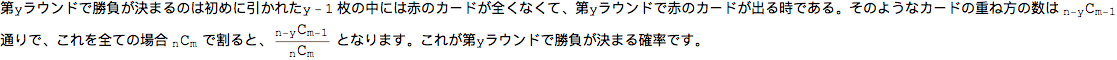
このように考えると、先手のAが負ける確率は 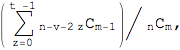ただし、

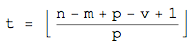
例題の中で紹介したパスカルの三角形的な図形は、先手の負ける確率が組み合わせの数で決まることから生まれます。なお、このカードゲームの詳しい理論に関しては、私達のグループのメンバーと先生が出版した論文を参照してください。

改変と研究

このように、初めの問題の数字やルールを変えるだけでここまで研究を進めることができました。

問題をじっくりと調べて、変更できることを見つけ、そこを変えると新しい事実が見つかります。

私達はこの問題に1992から、2007,2017,2018と長い期間をかけています。そして、近年になるに従って、研究の進みが早くなっています。それは、問題の部分変更で新しい研究ができることが、2007年くらいからはっきりとわかってきたからです。

新しい数学の公式を発見するというと、すごく難しく思えます。でも、既にある問題を少し変えるというと簡単に聞こえます。「少し変えるだけ」でここまでできるのです。

 

参考文献

[1] 宮寺良平, 坂口宗敏, 増田正幸, ロシアンルーレットの数学的理論, 大阪数学教育雑誌 26 (1997).

[2] Matsui, H., Minematsu, D., Yamauchi T., Miyadera, R.: Pascal-like triangles and Fibonacci-like sequences, Mathematical Gazette, (2010).

[3] Miyadera,R.,Suzuki,S., and etc., Generalized Pascal-Like Triangles, JCDCG^3 2018 (The 21th Japan Conference on Discrete and Computational Geometry, Graphs, and Games), Manila, August, 2018.

[4] Miyadera,R.,and etc., "Pascal-Like Triangles and Fibonacci-Like Sequences", JCDCG^3 2017, Tokyo, August, 2017.