日本語

Gallery

Higeo

”They are beautiful figures and numerical expressions originated from our research”

Pyon

"Beautiful?"

Penta

"What's the beauty in math?"

Higeo

"OK! I'll show you."

We will introduce beautiful figures in our research originated from our research. High school students' ideas make wonderful figures like this. They are made from mathematical theories of ours, and they are fantastic!

99999…99999999…999

I will introduce the research on 99999…99999999…999. Our teacher and his students found this when they ware playing Mathematica.

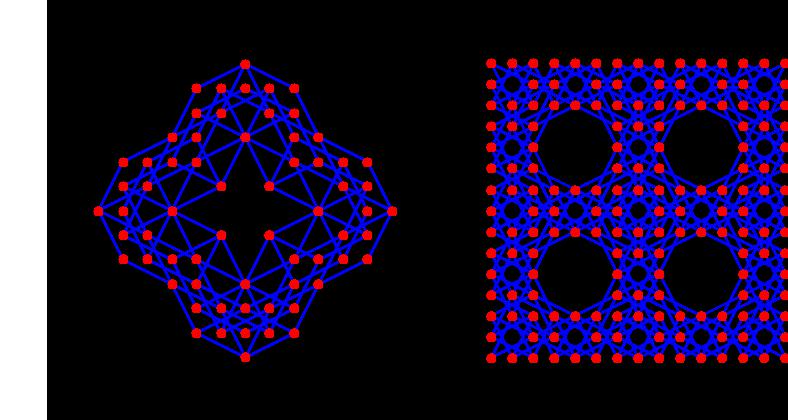
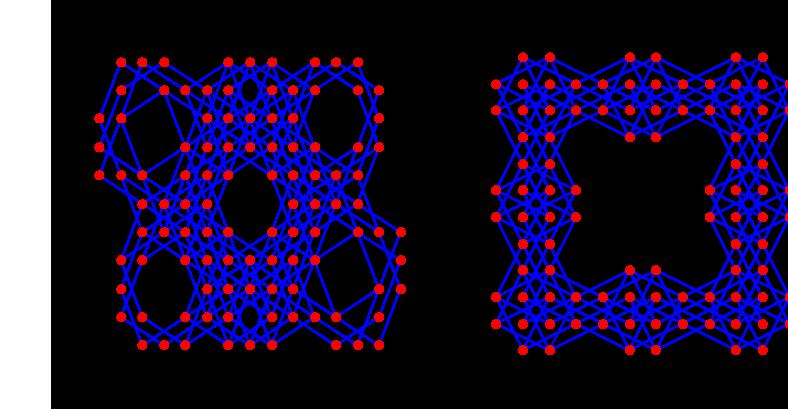
Here, we are using 10000digits number, and under certain condition we find a beautiful half moon figure.

This is our original figure, and there is none that is similar to this in the world. We made an animation using this figure.

Please compare the number above the figure and the shape of the figure.

As for the detailed explaination on this figure, see our paper published by the Mathematical Institute of the Serbian Academy of Sciences and Arts, Belgrade.

We studied the same figure from a different perspective. See the following paper that is published by Archmede that is a national paper on mathematics and mathematics education.

 

Triangles that are similar to Pascal's triangle

Here, we present triangles that are similar to Pascal's triangle, and they are originated from a card game. We colored odd numbers and even numbers with different colors.

If we increase the number of players, the triangle changes. Then, we can make an animation with these triangles. This is a very unique animation of fractal triangles. The well known scientist S. Wolfram found this very interesting, and he highly evaluated our research.

As for the detailed explaination on this figure, see our paper published by the Mathematical Institute of the Serbian Academy of Sciences and Arts, Belgrade. 。

As for the detailed explaination on this figure, see the following paper published by Mathematical Gazette.

Knight Tour

There is a well known puzzle called Knight Tour. As for an explanation, you can find one in Wiki.

Here we tried to make beautiful figure of Knight tour instead of soloving difficult problems.

We were the first to try to make a beautiful figure. Note that this is not an animation.

　　

　　

　　

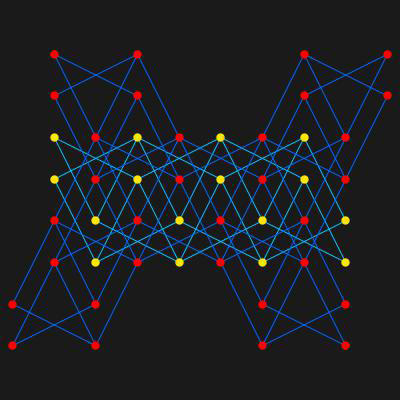
A Knight Tour with two independent path often produce a very beautiful figure.

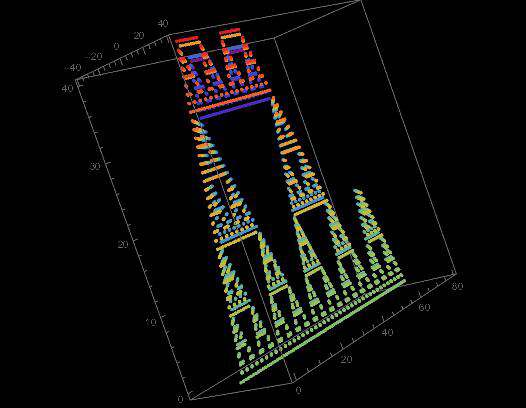
The following article is ours that is published by Italian online math journal.

Chocolate Game

There is a problem called Chocolate Game.

This game has been presented in Mathematical Gazette as a problem for the reader, but we changed some parts of the problem to make a very interesting variant of game of nim. We managed to write some papers that were published by some international math magazine. The previous player's winning positions of this chocolate game can make a beautiful fractal figure. This is not an animation.

　　

　　

Our article is on the following American Mathematics magazine.

Beautiful figure produced by square root and periodic numbers.

　If you put periodic numbers into square root, you get the following numbers.

Some students discovered this when they were playing with mathematics software Mathematica. This is not an animation.

　　

　　

This discovery is on the following Italian online mathematics magazine.

Origami cup problem

Here, we present a origami cup that is our discovery. We tried to make a cup as big as possible using a square sheet of paper. There is a very interesting animaton of the making of this cup. The application of this cup has not been discovered.

This is very unique creation, and our group represented Asia in Google Science Fair, and this cup was introduced in a TV program.

　　　

Appendix

Some characters that appeared in this web contents.

If you find these charecters attractive, please watch the following animation movie. Animarion 1 is the winner of silver medal in Japan Wide high school movie contest.

Jump to animation 1

　　　

Jump to animation 2

　　　

Jump to animation 3