Gallery

Higeo
”They are beautiful figures and numerical expressions originated from our research”

Pyon
"Beautiful?"

Penta
"What's the beauty in math?"

Higeo
"OK! I'll show you."
We will introduce beautiful figures in our research originated from our research. High school students' ideas make wonderful figures like this. They are made from mathematical theories of ours, and they are fantastic!
99999…99999999…999
I will introduce the research on 99999…99999999…999. Our teacher and his students found this when they ware playing Mathematica.
Here, we are using 10000digits number, and under certain condition we find a beautiful half moon figure.
This is our original figure, and there is none that is similar to this in the world. We made an animation using this figure.
Please compare the number above the figure and the shape of the figure.
As for the detailed explaination on this figure, see our paper published by the Mathematical Institute of the Serbian Academy of Sciences and Arts, Belgrade.
Reference
Daisuke Minematsu, Satoshi Hashiba and Ryohei Miyadera, An animation of numbers 999...999n.
Mathematics Art, Visual Mathematics
Link to the referenceWe studied the same figure from a different perspective. See the following paper that is published by Archmede that is a national paper on mathematics and mathematics education.
Reference
R. Miyadera and Y. Kotera: Una Bella Curva Che Troviamo in Connessione con lo Sviluppo di, Archimede, 2, 2005
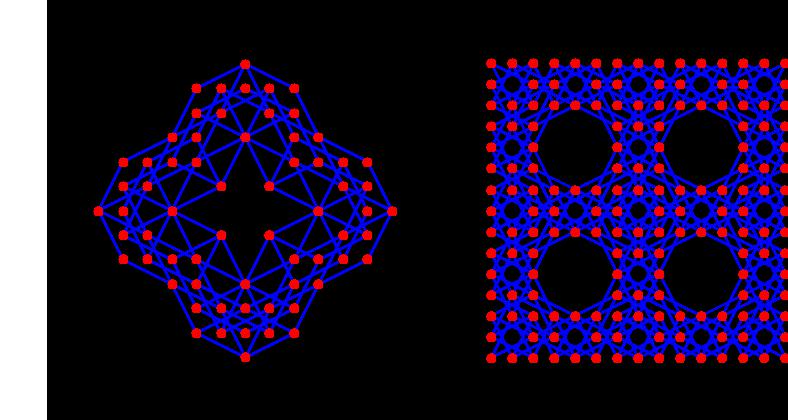
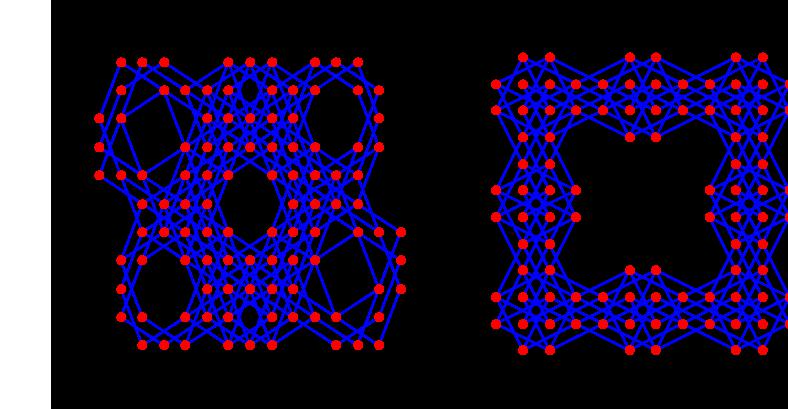
Triangles that are similar to Pascal's triangle
Here, we present triangles that are similar to Pascal's triangle, and they are originated from a card game. We colored odd numbers and even numbers with different colors.
If we increase the number of players, the triangle changes. Then, we can make an animation with these triangles. This is a very unique animation of fractal triangles. The well known scientist S. Wolfram found this very interesting, and he highly evaluated our research.
As for the detailed explaination on this figure, see our paper published by the Mathematical Institute of the Serbian Academy of Sciences and Arts, Belgrade. 。
Reference
Tomohide Hashiba, Yuta Nakagawa, Toshiyuki Yamauchi, Hiroshi Matsui, Satoshi Hashiba, Daisuke Minematsu; Munetoshi Sakaguchi; Ryohei Miyadera, Pascal like triangles and Sierpinski like gaskets
Visual Mathematics (2007) Issue: 33, ISSN: 1821-1437
As for the detailed explaination on this figure, see the following paper published by Mathematical Gazette.
Reference
H. Matsui, D. Minematsu, T. Yamauchi and R. Miyadera, Pascal-like triangles and Fibonacci-like sequences
Volume 94, Issue 529, March 2010 , pp. 27-41
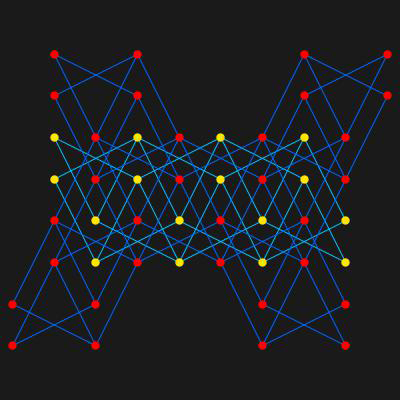
Knight Tour
There is a well known puzzle called Knight Tour. As for an explanation, you can find one in Wiki.
Here we tried to make beautiful figure of Knight tour instead of soloving difficult problems.
We were the first to try to make a beautiful figure. Note that this is not an animation.
A Knight Tour with two independent path often produce a very beautiful figure.

The following article is ours that is published by Italian online math journal.
Reference
New Knight's Tour Puzzles and Graphs
Some neat variants of the famous Knight's Tour
by Yuya Kakoi, Naoki Saida, Kazuki Takeshima, Yuma Kunimori, Takashi Kajimoto, Hiroshi Matsui, Toshiyuki Yamauchi, Naoyuki Totani and Ryohei Miyadera.
Jump to Online magazineChocolate Game
There is a problem called Chocolate Game.
This game has been presented in Mathematical Gazette as a problem for the reader, but we changed some parts of the problem to make a very interesting variant of game of nim. We managed to write some papers that were published by some international math magazine. The previous player's winning positions of this chocolate game can make a beautiful fractal figure. This is not an animation.
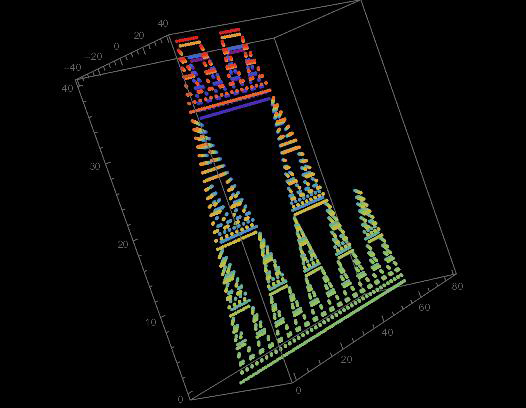
Our article is on the following American Mathematics magazine.
Reference
R. Miyadera, S. Nakamura, Y. Okada, R. Hanafusa, and T. Ishikawa,
Chocolate Games -How High School Students Discovered New Formulas Using Mathematica-
Mathematica Journal, Volume 15, 2013. Jump to the Reference
Beautiful figure produced by square root and periodic numbers.
If you put periodic numbers into square root, you get the following numbers.
Some students discovered this when they were playing with mathematics software Mathematica. This is not an animation.

This discovery is on the following Italian online mathematics magazine.
Reference
In this site, you can find this fact when you look for name "miyadera" that is the name of advisor of this group. This fact is with his name and his students' names.
Archimedes' Laboratory online Jump to Reference
Origami cup problem
Here, we present a origami cup that is our discovery. We tried to make a cup as big as possible using a square sheet of paper. There is a very interesting animaton of the making of this cup. The application of this cup has not been discovered.
This is very unique creation, and our group represented Asia in Google Science Fair, and this cup was introduced in a TV program.
Appendix
Some characters that appeared in this web contents.



If you find these charecters attractive, please watch the following animation movie. Animarion 1 is the winner of silver medal in Japan Wide high school movie contest.
Jump to animation 1Jump to animation 2
Jump to animation 3
